




| |
 "Квадрат,
построенный на гипотенузе прямоугольного
треугольника, равновелик сумме квадратов,
построенных на его катетах".
Простейшее доказательство теоремы получается в
простейшем случае равнобедренного
прямоугольного треугольника. Вероятно, с
него и начиналась теорема. В самом деле,
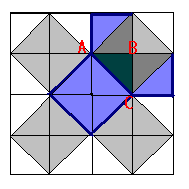
достаточно просто посмотреть на мозаику
равнобедренных прямоугольных
треугольников (рис. 1), чтобы убедиться в
справедливости теоремы. Например, для ΔABC:
квадрат, построенный на гипотенузе АС,
содержит 4 исходных треугольника, а
квадраты, построенные на катетах,— по два.
Теорема доказана. "Квадрат,
построенный на гипотенузе прямоугольного
треугольника, равновелик сумме квадратов,
построенных на его катетах".
Простейшее доказательство теоремы получается в
простейшем случае равнобедренного
прямоугольного треугольника. Вероятно, с
него и начиналась теорема. В самом деле,
достаточно просто посмотреть на мозаику
равнобедренных прямоугольных
треугольников (рис. 1), чтобы убедиться в
справедливости теоремы. Например, для ΔABC:
квадрат, построенный на гипотенузе АС,
содержит 4 исходных треугольника, а
квадраты, построенные на катетах,— по два.
Теорема доказана.
|

